As you may recall, a mixed number consists of an integer and a proper fraction. Any mixed number can also be written as an improper fraction, in which the numerator is larger than the denominator, as shown in the following example:

Example 1

To add mixed numbers, we first add the whole numbers together, and then the fractions.

If the sum of the fractions is an improper fraction, then we change it to a mixed number. Here's an example. The whole numbers, 3 and 1, sum to 4. The fractions, 2/5 and 3/5, add up to 5/5, or 1. Add the 1 to 4 to get the answer, which is 5.

Example 2

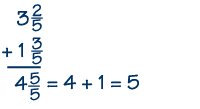
If the denominators of the fractions are different, then first find equivalent fractions with a common denominator before adding. For example, let's add 4 1/3 to 3 2/5. Using the techniques we've learned, you can find the least common denominator of 15. The answer is 7 11/15.

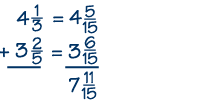
Subtracting mixed numbers is very similar to adding them. But what happens when the fractional part of the number you are subtracting is larger than the fractional part of the number you are subtracting from?

Here's an example: let's subtract 3 3/5 from 4 1/3. First you find the LCD; here it's 15.

4 1/3 - 3 3/5 4 5/15 - 3 9/15	Write both fractions as equivalent fractions with a denominator of 15.
3 + 1 5/15 - 3 9/15 3 + 20/15 - 3 9/15	Since you're trying to subtract a larger fraction from a smaller one, you need to "borrow" a one from the integer 4, change it to 15/15, and add it to the fraction.
3 20/15 - 3 9/15 11/15	Now the problem becomes 3 20/15 minus 3 9/15 and the answer is 11/15.

 

back to top