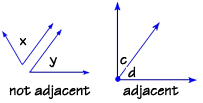
Adjacent means "next to." But we use this word in a very specific way when we refer to adjacent angles. Study these two figures. Only the pair on the right is considered to be adjacent, angles c and d. Adjacent angles must share a common side and a common vertex, and they must not overlap each other.

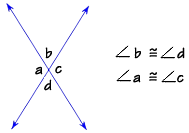
Vertical angles are pairs of angles formed by two intersecting lines. Vertical angles are not adjacent angles—they are opposite each other. In this diagram, angles a and c are vertical angles, and angles b and d are vertical angles. Vertical angles are congruent.

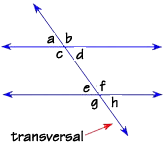
These two lines are parallel, and are cut by a transversal, which is just a name given to a line that intersects two or more lines at different points. Eight angles appear, in four corresponding pairs that have the same measure, so therefore are congruent.

These four corresponding pairs are:

angles a and e
angles c and g
angles b and f
angles d and h

The angles that lie in the interior area, or the area between the two lines that are cut by the transversal, are called interior angles. Angles c, d, e and f are interior angles. Angles a, b, g, and h lie in the exterior area, and they are called "exterior angles."

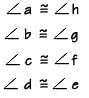
We call angles on opposite sides of the transversal alternate angles. Angles c and f, and d and e, are alternate interior angles. Angles a and h, and b and g, are alternate exterior angles. Note that these alternate pairs are also congruent.

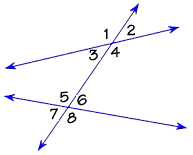
When a transversal cuts two lines that are not parallel, as shown here, it still forms eight angles—four corresponding pairs. However, the corresponding pairs are not congruent as occurs with parallel lines.

back to top