Study these two triangles. How are they alike? If we rotated the pink triangle and slid it on top of the green one, the two would fit on top of each other exactly. All the sides and all the angles are equal, so these two triangles are congruent.

If two figures are congruent, then their corresponding parts are congruent. Let's look at the corresponding parts of triangles ABC and DFE.

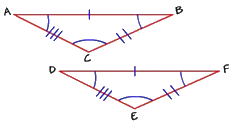
A triangle has three sides and three angles. If two triangles are congruent, then the sides and angles that match are called corresponding parts. Here, angle A corresponds to angle D, angle B corresponds to angle F, and angle C corresponds to angle E. Side AB corresponds to side DF, side BC corresponds to side FE, and side CA corresponds to side ED.

Congruent figures are named in the order of their corresponding parts. For these triangles, we say "triangle ABC is congruent to triangle DFE," not "triangle DEF," because vertex A corresponds to vertex D, vertex B corresponds to vertex F, and vertex C corresponds to vertex E.

The lines crossing the sides (sometimes called "hash marks") are another way to keep track of which side corresponds to another. The side with one hash mark in triangle ABC corresponds to the side with one hash mark in triangle DFE.

How can we tell if two triangles are congruent? Just "eyeballing" them is not good enough, because our eyes can play tricks on us. One way is to trace around one of the triangles and place it over the other. If the angles and sides match exactly, then the two are congruent. But there is another way to tell. If two triangles have congruent corresponding parts, then the triangles are congruent triangles.

You can measure the corresponding parts. If they are all congruent, then the triangles are congruent.

These principles and rules of congruence hold true for any polygon.