
 |
| Home | Teacher | Parents | Glossary | About Us | |||||||||||
|
|
|||||||||||
|
|
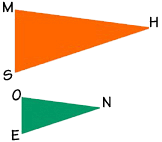
Let's look at the corresponding parts of these two triangles, triangle MHS and triangle ONE. Are the corresponding sides equal? How about the corresponding angles?
These triangles are not congruent, because the corresponding sides are obviously not equal. But they are somehow alike, aren't they? They have the same shape.
What about their angles? Are they equal? If we put triangle ONE on top of triangle MHS, we could compare each angle, and we would find that the corresponding angles are all congruent. This gives us the definition of similar triangles: if the corresponding angles of two triangles are congruent, then the triangles are similar.
Not only are the corresponding angles the same size in similar polygons, but also the sides are proportional. We can use the ratios called proportions to help us find missing values.
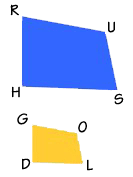
Here are two quadrilaterals: RUSH and GOLD. Are they similar? If we measured the angles, we would find that the corresponding angles are congruent. Therefore, these quadrilaterals are similar.
Since we know that they are similar, we also know that their sides are proportional. We can set up proportions between the sides, like this:
![]()
Let's use a proportion to find the length of segment OL, given the other lengths shown here.
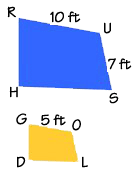
We can set up the problem like this. We read this proportion as "OL is to US as GO is to RU."
If we substitute the values of the segment lengths, we get this proportion.
![]()
Now we can use cross products to solve for the length of OL. We multiply the extremes and the means together, and solve for n.
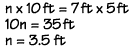
| Homework Help | Geometry | Relations and Sizes | |||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||