You've already met the right triangle in an earlier lesson. Make friends with him! He is one of the most popular polygons in existence, mainly because of his problem-solving abilities.

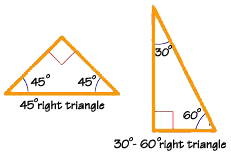
A right triangle has one angle equal to 90 degrees. A right triangle can also be an isosceles triangle--which means that it has two sides that are equal. A right isosceles triangle has a 90-degree angle and two 45-degree angles. This is the only right triangle that is an isosceles triangle. This version of the right triangle is so popular that plastic models of them are manufactured and used by architects, engineers, carpenters, and graphic artists in their design and construction work.

Another interesting right triangle is the 30-60-90 degree triangle. The ratio of this triangle's longest side to its shortest side is "two to one." That is, the longest side is twice as long as the shortest side. It too is manufactured in plastic and widely used in design, drawing, and building applications.

You can find an endless number of examples of right triangles. One of the most famous is the "3, 4, 5 triangle."

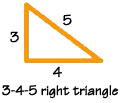
The Egyptians used this triangle for land surveying. Some believe that they also used it to help design their pyramids. Whether they did or not, the 3-4-5 triangle is still used by surveyors. Carpenters and woodworkers also use it to make their corners square.

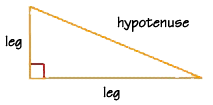
Pythagoras was a Greek mathematician who lived about 2500 years ago, and who developed the most famous formula in geometry, possibly in all of mathematics! He proved that, for a right triangle, the sum of the squares of the two sides that join at a right angle equals the square of the third side. The third side--the side opposite the right angle--is called the hypotenuse of the right triangle. The two shorter sides are usually called "legs."

This formula is called the Pythagorean Theorem in honor of Pythagoras. It is usually written as the equation below, where a and b are the measures of the legs of the triangle and c is the measure of the hypotenuse.

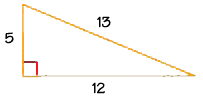
Let's try out the Pythagorean Theorem using this right triangle with sides of 5 and 12 cm, and a hypotenuse of 13 cm. We can verify that the Pythagorean Theorem is true by substituting in the values. The square root of 169 is 13, which is the measure of the hypotenuse in this triangle.

The Pythagorean Theorem has many uses. You can use it to verify whether or not a triangle is a right triangle. Or you can use it to find the missing measures of sides. Let's use the Pythagorean Theorem to find the missing measure of the leg of the right triangle SAM.

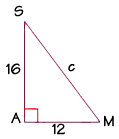
Substitute the values into the formula and perform the calculations, like this. We find that the square of the hypotenuse, or c squared, is equal to 400. To find c, we take the square root of 400, which is 20. This is the value we're looking for, the missing measure of the leg,