Three-dimensional figures - Prisms

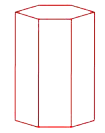
A prism is a polyhedron that has two congruent parallel polygons as its bases. The other faces of a prism are parallelograms, most often rectangles. A prism is named for the shape of its base. For instance, this prism is called a hexagonal prism, because its two bases are hexagons.

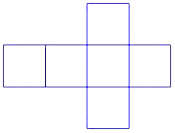
Visualizing three-dimensional figures is an important part of geometry, and it helps to build mental math muscle. Study this two-dimensional pattern. If we folded its sides together to form a space figure in three dimensions, what figure would we get? Can you visualize how the pieces would fit together?

This figure is the familiar cube, which is a type of rectangular prism. The cube is also called a "regular hexahedron," because it has 6 congruent faces. "Hexa" means six in Greek--there's one of those Greek names again!

All space figures have volume. You can find the volume of any prism using this formula:

V = Bh

where B equals the area of the base of the prism and h is its height. Imagine the base passing through the entire prism like an elevator going up. The space that the base passes through is the volume of the prism.

The units of volume are called "cubic units." Cubic feet, cubic meters, cubic inches, cubic yards, cubic centimeters--these are all examples of units of volume. They can all be written as powers of 3, because they have three dimensions.

Examples of units of volume:
cubic feet (ft³)
cubic inches (in³)
cubic yards (yd³)
cubic meters (m³)
cubic centimeters (cm³)

Given the dimensions shown in the figure, let's compute the volume of this prism.

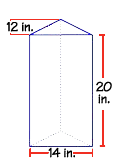
First we have to find the area of the triangle that forms the base of this prism. The area of a triangle is one-half the base of the triangle times the height of the triangle. Don't get the height of the triangle and the height of the prism mixed up! The triangle has a base of 14 inches and a height of 12 inches. If we substitute these values into the formula, we get 84 square inches for the area of the triangle.

The height of the prism is 20 inches. If we substitute the values into the volume formula, we find that the volume of the prism is 1,680 cubic inches.