a circle
|
|
Definition:
A circle is the locus of all points equidistant from a central point.
|
Definitions Related to Circles
|
arc: a curved line that is part of the circumference of
a circle
chord: a line segment within a circle that touches 2
points on the circle.
circumference: the distance around the circle.
diameter: the longest distance from one end of a circle
to the other.
origin: the center of the circle
pi ( ): A
number, 3.141592..., equal to (the circumference) / (the diameter)
of any circle.
radius: distance from center of circle to any point on
it.
sector: is like a slice of pie (a circle wedge).
tangent of circle: a line perpendicular to the radius
that touches ONLY one point on the circle.
|
Diameter = 2 x radius of circle
Circumference of Circle = PI x
diameter = 2 PI x radius
where PI =
= 3.141592...
Area of Circle:
area = PI r2
Length of a Circular Arc: (with central
angle  )
if the angle is in
degrees, then length = x
(PI/180) x r
if the angle is in
radians, then length = r x
Area of Circle Sector: (with central
angle )
if the angle is in
degrees, then area = (/360)x
PI r2
if the angle is in
radians, then area = ((/(2PI))x
PI r2
Equation of Circle: (Cartesian coordinates)
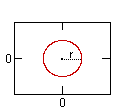
for a circle with center (j, k) and radius (r):
(x-j)^2 + (y-k)^2 = r^2
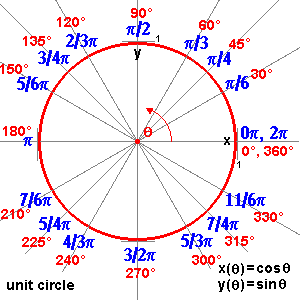
Equation of Circle: (polar coordinates)
for a circle with center (0, 0): r()
= radius
for a circle with center with polar coordinates: (c,  )
and radius a:
r2 - 2cr cos(
- ) + c2 = a2
Equation of a Circle: (parametric coordinates)
for a circle with origin (j, k) and radius r:
x(t) = r cos(t) + j y(t)
= r sin(t) + k
|
