The word polygon is a combination of two Greek words: "poly" means many and "gon" means angle. Along with its angles, a polygon also has sides and vertices. "Tri" means "three," so the simplest polygon is called the triangle, because it has three angles. It also has three sides and three vertices. A triangle is always coplanar, which is not true of many of the other polygons.

A regular polygon is a polygon with all angles and all sides congruent, or equal. Here are some regular polygons.

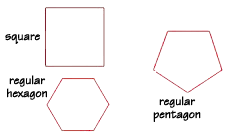
We can use a formula to find the sum of the interior angles of any polygon. In this formula, the letter n stands for the number of sides, or angles, that the polygon has.

sum of angles = (n – 2)180°

Let's use the formula to find the sum of the interior angles of a triangle. Substitute 3 for n. We find that the sum is 180 degrees. This is an important fact to remember.

To find the sum of the interior angles of a quadrilateral, we can use the formula again. This time, substitute 4 for n. We find that the sum of the interior angles of a quadrilateral is 360 degrees.

sum of angles = (n – 2)180°
= (4 – 2)180° = (2)180° = 360°

Polygons can be separated into triangles by drawing all the diagonals that can be drawn from one single vertex. Let's try it with the quadrilateral shown here. From vertex A, we can draw only one diagonal, to vertex D. A quadrilateral can therefore be separated into two triangles.

If you look back at the formula, you'll see that n – 2 gives the number of triangles in the polygon, and that number is multiplied by 180, the sum of the measures of all the interior angles in a triangle. Do you see where the "n – 2" comes from? It gives us the number of triangles in the polygon. How many triangles do you think a 5-sided polygon will have?

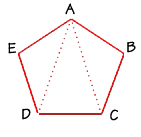
Here's a pentagon, a 5-sided polygon. From vertex A we can draw two diagonals which separates the pentagon into three triangles. We multiply 3 times 180 degrees to find the sum of all the interior angles of a pentagon, which is 540 degrees.

sum of angles = (n – 2)180°
= (5 – 2)180° = (3)180° = 540°

Related Links:
Polygon definitions, p olygon formulas (area, perimeter) and polygon names (Tables and Formulas)