
 |
| Home | Teacher | Parents | Glossary | About Us | |||||||||||
|
|
|||||||||||
|
|
Proof of 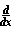 f(g(x)) =
f(g(x)) = 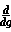 f(g) * f(g) *
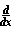 g(x)
from the definition g(x)
from the definition
We can use the definition of the derivative: Therefore, 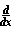 f(g(x))
can be written as such: f(g(x))
can be written as such:
df/dx * 1/(dg/dx) = [ (f(g(x+d) - f(g(x))/d ] * [ d/(g(x+d) - g(x)) ] df/dx = df/dg * dg/dx |
|
||||||||||||||||||||
|
|